Glencore prevails in the Cobar copper transfer pricing dispute, but should it have?

By Dr. J. Harold McClure, New York City

As reported in MNE Tax, the High Court of Australia denied the Australian Taxation Office (ATO) the opportunity to appeal its transfer pricing litigation with Glencore on May 21 (The Commissioner of Taxation of the Commonwealth of Australia v Glencore Investment Pty Ltd [2021] HCATrans 98). As such, the High Court let the November 6, 2020, decision of the Federal Court of Australia stand. This represented a win for Glencore over the ATO over intercompany pricing issues between Glencore’s Cobar copper mining affiliate and its Swiss parent.

In its plea before the High Court, the ATO made several arguments, including that the representatives of Glencore presented no evidence with respect to the “needs and risk appetites” of the counterparties to the intercompany transaction. The ATO noted how Glencore’s case turned upon how the issue of risk might bear upon the ascertainment of an arm’s length price. Despite this argument, the High Court rejected the call for an appeal by the High Court of the Federal Court decision.

I have in the past noted concerns that the ATO asked the wrong question while noting that the transfer pricing treatment of smelting costs for the period from 2007 to 2009 may have shifted income from the Cobar mining affiliate to the Swiss parent. This issue requires an appropriate economic analysis that goes beyond both traditional transfer pricing approaches and some of my past musings to address the valid concerns of both the ATO and the taxpayer. My hope in this latest commentary is to offer a stronger framework for evaluating both the expected return issues and the role of risk-sharing based on some financial economics.

The basic facts and various arguments

Before 2007, the intercompany contract between the Swiss distribution affiliate and the Cobar mining affiliate only compensated the Swiss affiliate for its very modest marketing functions as the mining affiliate was responsible for paying for the actual cost of smelting. From 2007 to 2009, the Swiss affiliate paid third-party smelters and charged the mining affiliate 23 percent of revenue in a price participation arrangement.

Glencore emphasized that the new contract had risk-sharing properties that a mining affiliate might prefer. However, the Australian tax authority argued that the 23 percent discount under the new agreement was excessive and departed from an arm’s length standard, shifting substantial profits to the Swiss affiliate.

The trial court and the Federal Court rejected the premise that the ATO had the right to change the new contract to the form of the original contract. My previous writings on this controversy recognized that multinationals have the right to structure the form of contracts in any reasonable fashion, arguing that a more fruitful approach would have been to assert a discount lower than 23 percent. In fact, one ATO expert witness reasoned that an 8 percent discount rate would have covered the expected cost of smelting relative to the expected price of copper.

Glencore, however, noted that a mining affiliate would have been willing to sacrifice expected profits for a reduction in risk. The problem with this argument, as the ATO noted, was that the mining affiliate was being asked to sacrifice a considerable amount of expected profits. Geoff Morris, for example, noted in the RoyaltyStat blog:

the ATO’s view was that when Cobar entered into a contract with its parent after February 2007 implementing a new pricing formula, it significantly reduced its gross earnings from the sale of copper concentrate and received nothing in return. The ATO also argued that the taxpayer’s industry expert agreed that, based on price forecasts and Cobar’s own budget at the time, it was likely that Cobar was going to be worse off for the 2007 to 2009 years under the new pricing formula. The taxpayer, according to the ATO, had never demonstrated the benefits that justified giving up so much expected gross revenue. No party acting independently from its parent and at arm’s length would ever have agreed to such detrimental changes.

Paul McNab of DLA Piper noted in International Tax Review:

Essentially, the matter concerned intra-group arrangements for the sale of copper concentrate. The group member which was the actual seller is referred to as CMPL in the judgments. The costs and pricing formulas used by the parties varied over time, but changes made with effect from 2007 triggered the dispute. In the years under review, treatment costs and refining costs (TCRCs) were set at 23% of the copper price, which had the effect of sharing risk between the parties … The Commissioner’s argument, the court said, was “why would a party in the position of CMPL have agreed to such a debilitating change of terms” in February 2007. The court rejected this approach saying it was the wrong question (from paragraph 166).

Glencore justified this 23 percent gross margin by citing other price participation agreements. The ATO asserted, however, that these other agreements were not comparable to the intercompany contract. Melbourne area transfer pricing practitioner, Geoff Morris noted in his blog post that the evidence presented by the expert witnesses for both the ATO and Glencore arguing that the ATO failed to meet its burden of proof.

My prior arguments have been based on a belief that the ATO would have benefitted from a more complete economic modeling of the issues. While I have attempted to fill in the blanks in this respect, my previous writings have focused more on expected profits with no comparison to the value of risk reduction. My hope here is to take this additional step.

The expected cost of smelting relative to expected copper prices

Price participation arrangements base the smelter fee paid by the mining affiliate as a percentage (s) of the price of copper (C_p). In the intercompany arrangement, the Swiss affiliate paid third-party smelting companies for the actual cost of smelting copper (S_c). Smelting costs have shown considerable variability over time. Copper prices also exhibit considerable variability.

The expected profits for the Swiss affiliate would be given by s^.C_p – S_c. If third-party agents were risk-neutral, then the value of s in a price participation contract would be seen as the ratio of the expected cost of smelting to the expected copper price as expected profits would be zero:

s = S_c/C_p.

Francisco J. Díz-Borrego, María del Mar Miras-Rodríguez, and Bernabé Escobar-Pérez discuss the importance of forecasting smelter costs in the copper sector (“Looking for Accurate Forecasting of Copper TC/RC Benchmark Levels”, Complexity, April 1, 2019):

Forecasting copper prices has been the objective of numerous investigations. However, there is a lack of research about the price at which mines sell copper concentrate to smelters. The market reality is more complex since smelters obtain the copper that they sell from the concentrate that mines produce by processing the ore which they have extracted. It therefore becomes necessary to thoroughly analyse the price at which smelters buy the concentrates from the mines, besides the price at which they sell the copper. In practice, this cost is set by applying discounts to the price of cathodic copper, the most relevant being those corresponding to the smelters’ benefit margin (Treatment Charges-TC and Refining Charges-RC). These discounts are agreed upon annually in the markets and their correct forecasting will enable making more adequate models to estimate the price of copper concentrates, which would help smelters to duly forecast their benefit margin.

Their paper also provides annual data on treatment charges and refining charges from 2004 to 2017. Table 1 provides their data as well as a composite fee per pound of finished copper concentrate. Treatment charges are often reported as dollar per metric ton of raw copper used in the smelting process, while refining charges are expected in terms of cents per finished copper. Our calculation assumes one metric ton of raw copper eventually become 1100 pounds of finished copper. If treatment charges were $80 per metric tons and refining charges were $0.08 per pound, then overall smelting costs (S_c) would be 15.27 cents.

Table 1: Smelting costs – 2004 to 2017

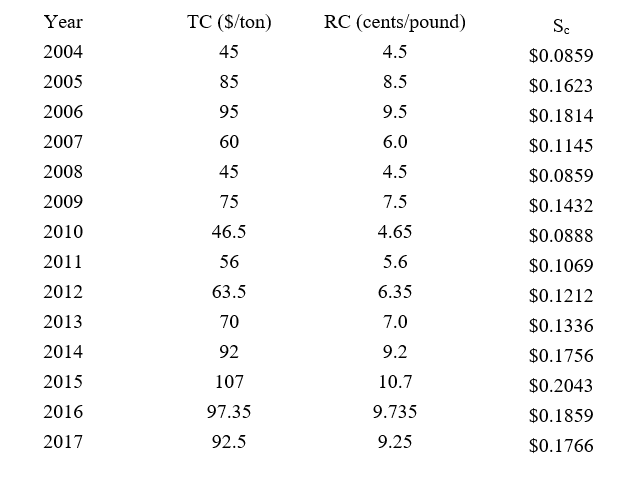
Table 1 shows the variability of smelting costs over the 2004 to 2017 period. These costs rose from 2004 to 2006, reaching $0.18 per pound in 2006. Actual smelting costs were much lower for the 2007 to 2013 period but were considerably higher for the 2014 to 2017 period.

The taxpayer’s experts presented two forecasts for smelting costs. Brook Hunt’s forecast for smelting costs over the 2007–2009 period averaged 15.8 cents per pound, while Glencore’s forecast averaged 19.2 percent. It is reasonable to assume that expected smelting costs would be $0.18 per pound, which was the actual costs observed in 2006. While we now know actual smelting costs were lower for this period, our economic model for price participation arrangements is based on expected costs.

Copper prices did not reach $1 per pound until December 2003 but soared to almost $4.50 per pound by early 2011. The rise in copper prices during the period after 2003 was a major issue in this litigation. Copper prices averaged $3.06 per pound during 2006 but fell during the early months of 2007 before rising to $3.65 per pound by October 2007. Copper prices since then have been highly volatile. The expert witnesses for the taxpayer had very different views on expected copper prices for the 2007 to 2009 period than the expert witnesses for the ATO. Actual prices averaged $2.95 per pound during this period, but one could imagine a claim that expected prices were as low as $2 per pound.

The testimony of Glencore’s experts suggested that copper prices were expected to be $2.25 per pound for the 2007 to 2009 period. While the average price of copper over this period was nearly $3 per pound, actual copper prices exceeded the forecasts available at the beginning of the relevant period.

Their testimony also suggested that the expected cost of smelting was $0.18 per pound. A risk-neutral model would suggest that the discount for smelting would be 8 percent, not 23 percent. If miners were risk-averse, they might negotiate somewhat higher price participation rates as a means to reduce risk but not a near tripling of the risk-neutral participation rate.

The risk/expected return argument and CAPM

Financial economists evaluate the expected return to assets for any enterprise as the sum of the risk-free rate and the appropriate premium for bearing operational risks. The capital asset pricing model (CAPM) was the original and most intuitive version of these models.

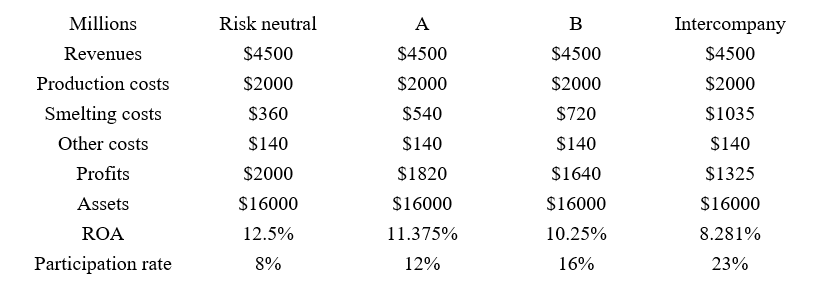
Consider the implications of CAPM for a copper mine that produces 2000 million pounds of copper concentrate per year. Table 2 assumes an expected price equal to $2.25 per pound, so expected revenue = $4.5 billion per year. Expected production costs = $1 per pound or $2 billion per year. The mine has to bear smelting costs as well as other (selling and shipping) costs.

Let’s assume that other costs represent $0.07 per pound or $140 million per year. Table 2 presents smelting costs as the participation rate (s) times revenue. If s = 8 percent, the expected smelting costs are $0.18 per pound or $360 million per year. If we also assume that the value of the mine is $16 billion, the $1 per pound or $2 billion per year in expected profits represents an expected return to assets (ROA) = 12.5 percent.

Table 2: Financial Modeling for the Mining Affiliate’s Expected Income

CAPM holds that the expected return to any asset (R_j) is given by:

R = R_f + β_j(R_m – R_f ),

where R_f = the risk-free rate, R_m = the expected return on the market portfolio of assets, and β = the beta coefficient for this particular asset. The beta coefficient measures the tendency of the asset’s return to move with unexpected changes in the return to the market portfolio. Beta coefficients are often estimated for the equity of publicly traded companies. Equity betas, which reflect both operational risk and leverage risk. Since our task is to estimate the expected return to assets rather than the expected return to equity, our beta estimates must be on a debt-free, unlevered, or asset basis. The asset beta is given by

We shall remove the effect of leverage on these equity betas (β_e):

β_a = β_e(E/(E + D) = β_a = β_e(E/A).

where D = debt, E = the market value of equity, and the market value of assets (A) = E +D.

New York University professor Aswath Damodaran provides rough estimates for the cost of capital by sector on his university website. The typical equity beta for the mining sector = 1.62, while the typical equity to asset ratio is 86.64 percent. As such a reasonable equity for the asset beta of a mining enterprise is β_a = 1.4.

If the premium for bearing market risk, then the premium for bearing operational risk in the mining sector is 7 percent. If we also assume a 5.5 percent risk-free rate, then the expected cost of assets for a mining affiliate is 12.5 percent.

This derivation assumes a mining affiliate that has not traded off expected return for a reduction in systematic risk, which is a reasonable assumption for a mining entity that does not engage in price sharing arrangements. The first column of our table represents such a mining enterprise. The other three columns explore various assumptions for the price sharing ratio to analyze how much of a reduction in expected return is implied for any assumption with respect to the price sharing ratio.

If the price ratio (s) is 23 percent, the mining affiliate’s expected return is only 8.28 percent, consistent with a risk premium of only 2.78 percent. The price sharing arrangement eliminates the uncertainty of actual smelting costs and presents a partial buffer with respect to commodity price risk. The mining affiliate would still bear both considerable price risk but also risks with respect to production and other costs. Reducing the risk premium by over 60 percent appears implausible, which is consistent with one of the ATO’s concerns.

The reduction in systematic risk, however, does warrant some sacrifice of expected return. If the price sharing ratio(s) ranges from 12 percent to 16 percent, the expected return ranges from 11.375 percent to 10.25 percent. The underlying premise that a mining entity would sacrifice between 16 percent to 32 percent of its risk premium to gain the risk reduction advantages of a price sharing arrangement is more plausible.

The fallacy of comparing gross margins for third party agreements

Glencore’s defense for the high price sharing percentage appears to be the percentages charged in six other pricing sharing arrangements. One of these arrangements was between two affiliates of BHP Billiton. In late 2003, a Peruvian copper mining affiliate named Tintaya SA entered into an agreement with BHP’s Singapore marketing hub, which was given a 25.5 percent discount for smelting costs. The Peruvian tax authorities challenged this intercompany arrangement arguing that the 25.5 percent discount was above the arm’s length standard.

The Australian tax authorities argued that the earlier contracts were not comparable to an agreement entered into during the beginning of 2007. The Redbank agreement was established around the same time that the Glencore intercompany agreement was revised. This agreement provided a 20 percent discount for Glencore. The Redbank agreement had a comparability difference, though, because Glencore was responsible for freight charges. Glencore’s Swiss affiliate also paid for shipping of Cobar copper but passed this cost onto the mining affiliate in the form of a freight allowance.

The other third-party agreements were established years before the intercompany agreement with the Cobar mining affiliate. A key argument made by the Australian tax authority was that market conditions during the 2007– 2009 period were fundamentally different from historical market conditions. Copper prices had risen dramatically. Over the 15-year period from January 1990 to December 2004, copper prices ranged from $0.60 per pound to $1.40 per pound averaging $0.965 per pound. Over the 15-year period from January 2005 to December 2019, copper prices ranged from $1.50 per pound to $4.50 per pound averaging $2.948 per pound. In addition, expected smelting costs may have been low relative to previous periods.

The following chart calculates the smelter fee per pound, assuming s = 23 percent under copper prices ranging from $0.50 per pound and $4.50 per pound. Profits are defined as the smelting fee minus the expected $0.18 cost of smelting. Note if actual copper prices were equal to the $2.25 forecast, the Swiss affiliate’s expected profits = 33.75 cents. We also know that actual copper prices were higher and that smelting costs fell below $0.18 per pound of copper. As such, the Swiss affiliate enjoyed considerable profits under the intercompany agreement. In fact, profits would have been positive as long as copper prices were $0.80 per pound or more.

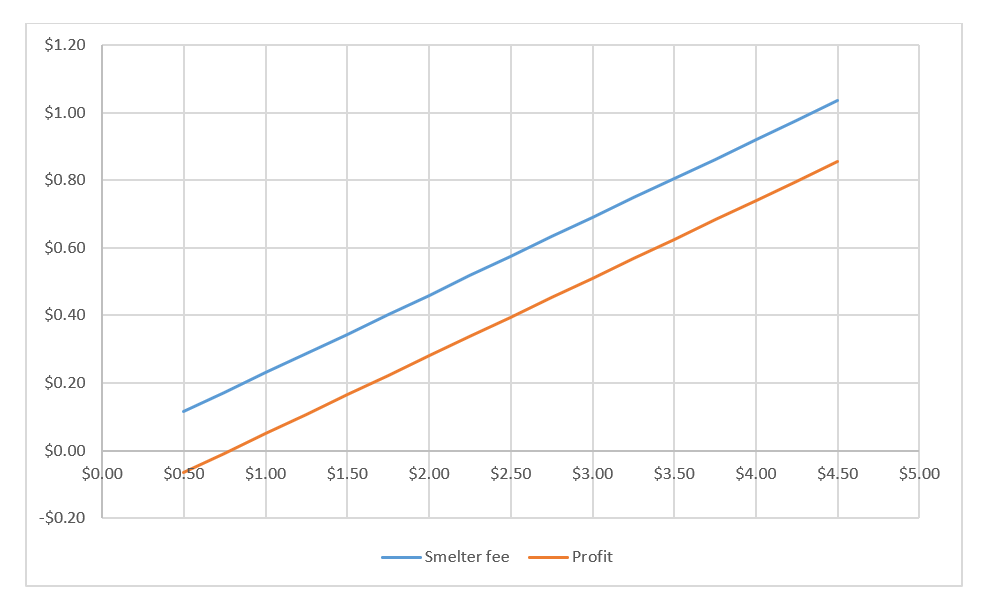
A 23 percent discount may have been rational for a price-sharing agreement negotiated in 2001 when expected copper prices were closer to $1 per pound. If expected smelting costs were $0.20 per pound as opposed to $0.18 per pound, expected profits would have been only 3 cents per pound. While the trading entity extending the price participation arrangement would have been entitled to upside potential if actual copper prices rose above our assumed $1 forecast, the trading affiliate would also be exposed to downside risk if actual prices fell below $1 per pound.

When viewed in terms of our economic model and given the history of copper prices over the past 30 years, any third-party agreement negotiated in 2001 would be expected to have a higher discount than the appropriate discount for the intercompany agreement covering the 2007 to 2009 period.

Concluding comments

In my December 9, 2020, discussion of this litigation in MNE Tax, I compared the risk-sharing properties of price sharing agreements to the commonly seen price participation agreements. As copper prices rise, price sharing agreements shift more profits away from the mining affiliate than price participation agreements. At the time of the change in Glencore’s intercompany agreement, mining multinationals were moving away from price participation agreements on the concern that these agreements were granting too much profit to the smelting companies.

The Australian courts, however, were sympathetic to Glencore’s risk-sharing arguments in this litigation. Even though taxpayers have the right to structure intercompany agreements in the fashion they choose, the quantitative question remains whether the 23 percent discount rate was arm’s length or excessive. A comparison of gross margins from third-party agreements would be convincing evidence only if the economic fundamentals were similar.

The evidence presented in this litigation suggests that the economic fundamentals differed fundamentally. The unanswered question in this litigation was how one might use these economic fundamentals to derive an appropriate discount.